深度学习教程──从感知器到深度网络
本文原作者是Java工程师Ivan Vasilev, 同时作者也开发了Java深度学习库, 大家可以去点赞. 这里我将根据我的理解, 作一记录.
近年来, AI又热门起来了. 她已经走出了学术研究的范畴, 现在Google, Microsoft, Facebook等巨头都拥有他们自己的团队, 而且已经完成了几轮融资.
一方面这源于对社交网络用户产生的大量原始数据分析的需求(毕竟赚钱才是本质, 社交只是形式, 呵呵), 另一方面则应归功于GPGPU带来的便宜而强劲的计算能力.
除此之外, 机器学习的最新动向—深度学习则为本次复兴注入了强劲的活力. 本教程将会带你:
. 从深度学习最简单的基本单元开始介绍 . 了解深度学习的核心概念与算法 . 最终用Java实践
机器学习30秒入门教程
可以进一步参考机器学习引论.
机器学习的一般过程如下:
- 我们手头有一些算法以及给了标记的
少量数据, 例如10张标记为1的狗狗图片和另外10张标记为0的非狗狗图片—这里谈到了标记, 请注意本教程主要考虑监督学习(supervised), 二元分类(binary classification). - 我们期望, 让算法
学习区分这些图片, 然后给一张新的图片, 算法能够正确判断出该图片是狗狗还是非狗狗.
这个例子其实非常具有代表性, 例如数据可以是症状而标签是患有某种疾病与否; 或者数据是手写的字母而标签是它们所代表的真实字母.
感知器:早起的深度学习算法
最早的有监督学习算法之一是关于感知器(perceptron)的, 它是神经网络的基本构成单元.
假设在平面上有$n$个点, 标记为0和1. 然后给你一个新的点, 让你猜测它的标签是0还是1, 这正是上面给出的例子的图形化. 我们应该怎么合理的猜呢?
方法之一可能是找出该点附件的标签, 然后将大多数标签定义为该点的标签. 然而一种更高明的方式是恰当的选取一条直线最好的区分这两类标签作为分类依据.
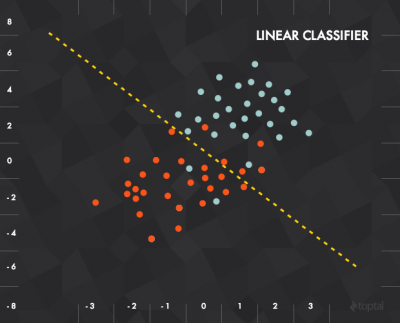 在本例中, 我们将每个数据表示为坐标$x=(x_1,x_2)$, 而我们的函数将在某条直线的下方取值为0, 上方取值为1. 也许你会问在直线上取值为啥?
在本例中, 我们将每个数据表示为坐标$x=(x_1,x_2)$, 而我们的函数将在某条直线的下方取值为0, 上方取值为1. 也许你会问在直线上取值为啥?
众所周知, 平面上直线的一般方程是
$$
f(x)=a x_1+bx_2+c,
$$
其中$a,b,c$是参数. 这个函数有时也称为变换函数(transfer function), 因为它将抽象的分类(在直线上方/下方)具体到$f(x)$的符号. 我们的输出函数(activation function)则定义为
$$
h(x)=\begin{cases}
1,& \text{if } f(x)>0\\
0,& \text{if } f(x)\leq0.
\end{cases}
$$
感知器的训练
训练感知器的过程是利用一堆训练样本计算每个样本的输出. 在每个样本计算之后, 调整权重$w$, 使得期望(目标)与实际输出的差异(这里是取绝对值)最小. 实际应用中还有其他误差函数, 例如根方差(mean square error), 但是基本的训练原理是一致的.
单一感知器的缺陷
深度学习中使用单一感知器有一个主要的局限性: 它只能学习线性分离函数. 这种局限性有多大? 通过下面的例子可以看出, 在下面的例中我们不可能使用线性分离函数来分类图形中的四个点:
 为了解决这一问题, 我们需要使用
为了解决这一问题, 我们需要使用多感知器, 也称之为前馈神经网络: 在实际应用中, 我们将把这些感知器组装成一个更加强大的学习机器.
前馈神经网络
神经网络其实仅仅是一些感知器的组合,它们之间连接的方式不同、而且使用的激活函数(activation function)也不同。
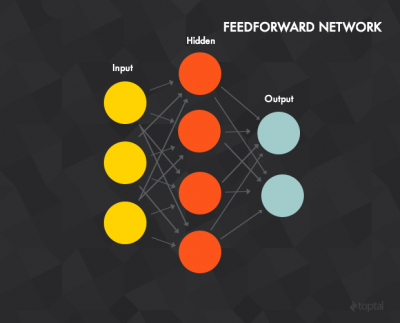 对于初学者,我们接下来讨论前馈神经网络,它具有如下性质:
对于初学者,我们接下来讨论前馈神经网络,它具有如下性质:
- 一个输入与输出以及一个或者多个隐式层。上图就是一个具有3个输入层、4个隐式层以及2个输出层的神经网络。这里的单位是神经元(neurons)或者单元(units)的个数。
- 每个神经元是如前说述的单感知器。
- 输入层的神经元将数据传递到隐式层、而隐式层的神经元将数据传入输出层。
- 每个神经元的链接具有权重$w$(类似于单一感知器的权重)。
- 处理输入数据时,你将输入向量“压入”(clamp)到输入层,将每个向量的分量作为输入层每个神经元的“输出”。在上图所表示的例子中,该神经网络可以处理3维输入向量(因为有3个输入单元)。例如,你输入向量$[7,1,2]$, 则你将输入层的最上面一个单元的输出设置为7, 中间一个设置为1,等等。这些值将利用带权的求和传输函数向前传播到隐式层,最终计算出输出(即激活函数)。
- 输出层计算它的输出和隐式层的方式是一样的。输出层的结果就是整个神经网络的输出。
突破线性性
如果我们的每个感知器都只能用线性激活函数,那会怎样呢?其结果是,我们神经网络的输出仍将是输入数据的某个线性函数,只不过在神经网络的传递过程中,经过很多不同权重的调整。换言之,线性激活函数的线性复合还是一个线性函数。如果我们只用线性激活函数,则前馈型神经网络并不比单一感知器更加强大,无论你用多少隐式层。
一系列线性函数的线性复合还是线性函数,故大多数的神经网络用的是非线性激活函数。
正因为如此,大多数神经网络使用非线性的激活函数,例如Logistic函数、tanh函数、 binary函数或者rectifier函数。如果不用非线性函数,那么神经网络只能学习其输入的线性组合这类函数。
感知器的训练
有监督训练多层感知器的深度学习中最常见的算法是所谓的反向传播算法(backpropagation)。其基本过程是:
- 将一个训练样本数据化然后沿着神经网络向前传播。
- 计算输出误差,通常是标准差: $$ E=\frac{1}{2}(t-y)^2, $$ 其中$t$是目标向量而$y$是实际的输出向量。当然,也可以使用其他的误差,但标准差是一个很好的选择。
- 利用随机负向梯度流的方法来最小化神经网络的误差。
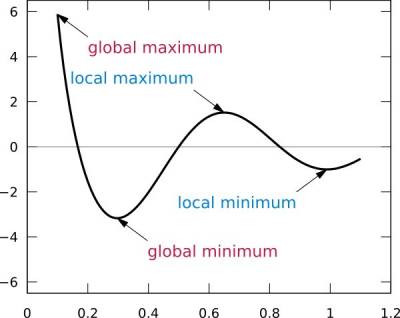 负向梯度流就是通常的,但在神经网络中,它是以输入参数为自变量而以训练后输出的误差为因变量的函数。因此,每个权重的最优解就是使得取这些权重时误差达到整体极小。在训练阶段,权重不断的以很小的步长更新(在每个训练样本之后或者小批量的多个样本之后更新),每次更新都使得输出与目标之间的误差减小。我们应该注意,这不是一件容易的事,如上图所示,你往往会在局部极小点处结束。例如,权重的值为0.6,则此时它需要变向0.4(言外之意,极有可能变向另一个方向,此时会在1左右达到局部极小值)。
负向梯度流就是通常的,但在神经网络中,它是以输入参数为自变量而以训练后输出的误差为因变量的函数。因此,每个权重的最优解就是使得取这些权重时误差达到整体极小。在训练阶段,权重不断的以很小的步长更新(在每个训练样本之后或者小批量的多个样本之后更新),每次更新都使得输出与目标之间的误差减小。我们应该注意,这不是一件容易的事,如上图所示,你往往会在局部极小点处结束。例如,权重的值为0.6,则此时它需要变向0.4(言外之意,极有可能变向另一个方向,此时会在1左右达到局部极小值)。
上图还只是最简单的情形,即误差只依赖于单一参数(权重)。一般而言,神经网络的误差依赖于每一个权重,因此实际的误差函数比上述例子复杂得多的多。
正是由于反向传播算法(backpropagation)方法的引入,它使得任何两个神经元之间的权重可以基于输出误差来更新。向后传播的推导本身有些复杂,但是给定节点的权重更新却很简单:
$$
\Delta w_i=-\alpha\frac{\partial E}{\partial w_i},
$$
这里, $E$是输出误差而$w_i$是神经元的第$i$个输入的权重。
本质上,我们的目的是沿着权重$i$的梯度方向移动。这里的关键词是,理所当然地,误差的导数,它并不总是容易计算的:对在超大神经网络中的随机隐式节点的随机权重,如何计算这一导数?
答案是:通过反向传播算法(backpropagation)。首先在输出单元计算误差,此时计算公式非常简单(基于预测输出与目标输出的差),而后以一种聪明的方式沿着神经网络反向传播,这样就让我们能够有效的更新在训练阶段的权重进而得到整体极小值。
隐式层
隐式层特别有意思。 由泛逼近定理(universal approximation theorem), 通过训练一个具有有限神经元的隐式层神经网络可以逼近任意随机函数。换言之,一个单一的隐式层已经足够强大到学习任何函数。也就是说,在实践中,通常我们利用更多的多隐式层(即更深的网)会使得神经网络学习得更好。
隐式层是神经网络存储训练数据内部抽象表示的地方。
隐式层是神经网络存储训练数据内部抽象表示的地方, 类似于人脑(超简单版)对现实世界的抽象表示。在本教程接下来的部分,我们将看到各种各样的隐式层。
神经网络的一个例子
你可以到这里(用Java实现)去看看一个简单的(4-2-3层)前馈型神经网络,通过testMLPSigmoidBP方法分类IRIS数据集的例子。这个数据集中包含了三类鸢尾属植物,特征包括花萼长度,花瓣长度等等。每一类提供50个样本给这个神经网络训练。特征被赋给输入神经元,每一个输出神经元代表一类数据集(“1/0/0” 表示这个植物是Setosa,“0/1/0”表示 Versicolour,而“0/0/1”表示 Virginica)。分类的错误率是2/150(即每分类150个,错2个)。
大神经网络面临的问题
一个神经网络可能含有多个隐式层:那时较高的层是对前一层的新的抽象。像我们之前提及的一样,你通常可以在实践中用大神经网络学得更好。
然而,增加隐式层的个数有如下两个难题:
- 零梯度:随着我们添加越来越多的隐含层,反向传播算法传递给较低层的信息会越来越无效。实际上,由于信息向后反馈,不同神经元间的梯度开始消失,对权重的依赖也会变弱。
- 过度拟合:这也许这是机器学习的核心难题。简言之,过度拟合指的是对训练数据有着过于好的识别效果,这往往会导至模型非常复杂。这样,会导致你的学习器对训练数据有非常好的识别较果,而对真实样本的识别效果则不甚理想。
下面我们来看一些深度学习的算法是如何解决这些难题的。
自动编码器
大多数机器学习入门都停止在前馈神经网络这一步。但是可能的网络空间远非如此──所以让我们继续。
自动编码器( Autoencoder)是典型的前馈型神经网络,旨在学习一个经过压缩的、分布表示(编码)的数据集。
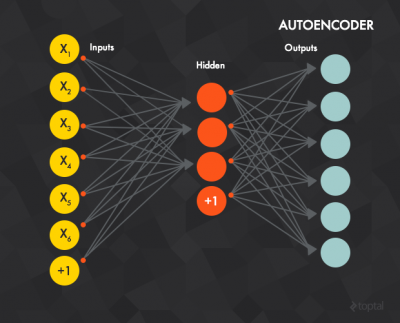 概念上来说,网络被训练成“重新生成”输入,即,输入以及目标数据是一样的。换句话说:你尝试着输出跟你输入的一模一样的东西,但在某种程度上经过了压缩。这是个容易让人迷糊的方法,所以让我们来看一个实例。
概念上来说,网络被训练成“重新生成”输入,即,输入以及目标数据是一样的。换句话说:你尝试着输出跟你输入的一模一样的东西,但在某种程度上经过了压缩。这是个容易让人迷糊的方法,所以让我们来看一个实例。
输入压缩:灰度图像
假设训练数据由像素28×28的灰度图片组成而且每一个像素值都赋给一个输入层的神经元(即输入层将有784个神经元)。之后,输出层也将同输入层一样有784个单元,并且每个输出元的目标值都将是图像中每一个像素的灰度值。
这样的结构背后的直觉是网络将不会学习如何在训练数据和标签之间建立一个“映射”关系,而是学习数据本身的内部结构和特征。(也因此,隐式层也称为特征探测器)。通常,隐式层神经元的个数要小于输入/输出层,这也就迫使神经网络只学习那些最为重要的特征,同时实现一个维度上的约化。
我们期望中间层具有较少的节点从而从抽象概念的层次学习数据,最终生成一个压缩过的表示。
实际上,我们期望中间层具有较少的节点从而从抽象概念的层次学习数据,最终生成一个压缩过的表示。这样在一定程度上能够捕捉到我们输入的关键特征。
流行性疾病
为了更进一步展示自编码器,让我们再来看一个应用。
在这个实例中,我们将使用一个简单的关于流感症状的数据集(想法属于这篇博客)。如果你有兴趣,这个实例的代码可在testAEBackpropagation方法中找到。
如下就是这个数据集如何被分解的:
- 这里有六个二进制输入特征。
- 前三个表示疾病的症状。比如,
1 0 0 0 0 0指这名患者体温过高,0 1 0 0 0 0代表咳嗽,1 1 0 0 0 0暗示着咳嗽和高体温,等等。 - 后三个特征是“相反”特征:当一名病人有其中一项症状,她或他就有更少的可能性患病。例如,
0 0 0 1 0 0暗示这名病人接种过流感疫苗,同时也存在将两个数据集特征结合起来的情况:0 1 0 1 0 0暗示着一个接种过疫苗的病人同时在咳嗽,诸如此类。
我们将考虑如下情况,当一个患者拥有前三种患病症状中至少两种症状时,他/她是患病的,同时如果有后三种“相反”症状里的两种,我们认他/她是健康的,比如:
111000,101000,110000,011000,011100= 生病000111,001110,000101,000011,000110= 健康
我们将会利用6个输入元和6个输出元以及仅2个隐藏元来训练自动编码器(通过反向传播算法)。
在经过数百次迭代之后,我们观察到当每一个“生病”样本被机器学习的网络表示出来时,两个隐层神经元中的一个(和每个“生病”样本相同的单元)总是表现出比其他神经元更高的激活值。相反的,当一个“健康”样本被表示,另一个隐藏神经元有更强的激活反应。
回到机器学习
本质上,我们的两个隐层神经元都是从流感症状数据集中学到了数据的压缩表示。为了看看这如何与学习相关联,我们回到过拟合的问题上来。通过训练我们的网络来进行数据的压缩表示,我们更偏爱一个较为简单的表示方法而不是一个十分复杂、有可能在训练数据上过拟合的理论模型。
在某种程度上,由于偏好这样更为简单的表示方法,我们也会尝试从一个更接近“真理”的意义上去学习数据。
有限Boltzmann机
下一个逻辑步骤是看看有限玻尔兹曼机Restricted Boltzmann machine (RBM),一个可以从它自身输入来学习概率分布的随机生成神经网络。
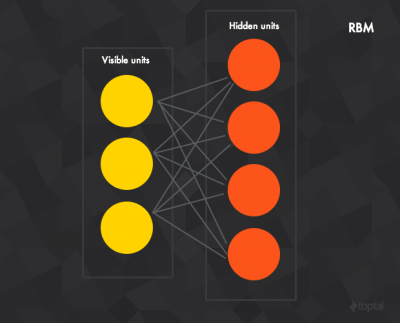 RBMS由隐藏层(hidden layer)、可见层(visible layer)、以及偏置层(bias layer)所组成。不同于前馈神经网络,在可见层和隐层之间的连接是无向的(值可以同时从隐层传到可见层,反之亦然)同时还是全连接的(给定层的每个神经元都会和下一层的每个神经元相连接——如果我们允许任意层次的任意神经元来连接到其他任何层次,那么就是
RBMS由隐藏层(hidden layer)、可见层(visible layer)、以及偏置层(bias layer)所组成。不同于前馈神经网络,在可见层和隐层之间的连接是无向的(值可以同时从隐层传到可见层,反之亦然)同时还是全连接的(给定层的每个神经元都会和下一层的每个神经元相连接——如果我们允许任意层次的任意神经元来连接到其他任何层次,那么就是玻尔兹曼机(Boltzmann)(并非有限玻尔兹曼机(restricted Boltzmann)))。
标准的RBM有二进制隐藏元和可见元:即是说在伯努利分布下神经元的激活值为0或者1,但是这里也有其他非线性的变量。
研究者们知晓RBMs已经有一定的年月,但最近关于对比分歧无监督训练算法的介绍又重新挑起了研究者们的兴趣。